სახლში » შინაური ცხოველების ბიზნესი » პრეზენტაცია თემაზე "ჯადოსნური კვადრატები". პრეზენტაცია "ჯადოსნური კვადრატები" პრეზენტაცია თემაზე Magic Squares

პრეზენტაცია თემაზე "ჯადოსნური კვადრატები". პრეზენტაცია "ჯადოსნური კვადრატები" პრეზენტაცია თემაზე Magic Squares

არისტეევი სერგეი

ეს ნამუშევარი პასუხობს კითხვებს: რა არის ჯადოსნური კვადრატები და როგორ ავაშენოთ? მოცემულია ლეგენდა ჯადოსნური კვადრატის შესახებ. ჩამოთვლილია ჯადოსნური კვადრატების აგების სხვადასხვა მეთოდი: ტერასული მეთოდი, კვადრატული ჩარჩო მეთოდი, Rouse-Ball მეთოდი, დელერის მეთოდი. მოცემულია პრაქტიკული მუშაობა ჯადოსნური კვადრატების შედგენაზე

ჩამოტვირთვა:

გადახედვა:

პრეზენტაციის გადახედვის გამოსაყენებლად შექმენით Google ანგარიში და შედით მასში: https://accounts.google.com

სლაიდის წარწერები:

ჯადოსნური სკვერები სერგეი არისტეევის ნამუშევარი, მე-5 კლასის მოსწავლე ასტრახანის ოლქის ლიმანსკის რაიონის მუნიციპალური საგანმანათლებლო დაწესებულების "კამიშოვსკაიას საშუალო სკოლის" ხელმძღვანელი ზოია ერდნიგორიაევნა გორიაევა, მათემატიკის მასწავლებელი სოფელ კამიშევოში, 2013 წ. გონებრივი ტანვარჯიში, რომელიც ავითარებს განლაგების, კომბინაციისა და სიმეტრიის იდეების გაგების უნარს“. ლეონარდ ეილერი

უპასუხეთ კითხვას: რა არის ჯადოსნური კვადრატი და როგორ ავაშენოთ იგი. პროექტის მიზანი: პროექტის მიზნები: ამ საკითხზე ლიტერატურის შესწავლა. გაეცანით ჯადოსნური კვადრატების ისტორიას. ისწავლეთ ჯადოსნური კვადრატების აგება სხვადასხვა გზით.

პრობლემის ფორმულირება ჯადოსნური კვადრატის ლეგენდა როგორ შევადგინოთ ჯადოსნური კვადრატები „ლო-შუ“ წესი Rouse-Ball მეთოდი ტერასული მეთოდი კვადრატული ჩარჩოს მეთოდი დელერის მეთოდი ან ლათინური კვადრატის მეთოდი დასკვნა. ლიტერატურის შინაარსი

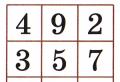
დაალაგეთ ნატურალური რიცხვები 1-დან 9-მდე ისე, რომ სვეტებისა და მწკრივების რიცხვების ჯამი იგივე იყოს. ამ პრობლემის გადასაჭრელად ისტორიას მივუბრუნდეთ. პრობლემის ფორმულირება

ძველ ჩინურ წიგნში "ჟე-კიმ" ("პერმუტაციების წიგნი") არის ლეგენდა, რომ იმპერატორმა ნუ, რომელიც ცხოვრობდა 4 ათასი წლის წინ, მდინარის ნაპირზე წმინდა კუ იხილა. მის ნაჭუჭზე თეთრი და შავი წრეების ნიმუში იყო. თუ თითოეულ ფიგურას ჩაანაცვლებთ რიცხვით, რომელშიც მითითებულია რამდენი წრეა, მიიღებთ შემდეგ ცხრილს: ლეგენდა ჯადოსნური კვადრატის შესახებ.

ამ მაგიდას აქვს შესანიშნავი თვისება. დავუმატოთ პირველი სვეტის რიცხვები: 4 +3 + 8=15. იგივე შედეგი მიიღება მეორე და მესამე სვეტების რიცხვების დამატებით. ის ასევე მიიღება სამივე სტრიქონიდან რომელიმე ნომრის მიმატებით. იგივე პასუხი, 15, მიიღება, თუ დავამატებთ თითოეული ორი დიაგონალის რიცხვებს: 4+5+6=8+5+2=15. ჩინელებს ეს ლეგენდა, ალბათ, მაშინ მოუგონიათ, როცა 1-დან 9-მდე რიცხვების განლაგება ასეთი შესანიშნავი თვისებით აღმოაჩინეს. მათ ნახატს "ლო-შუ" უწოდეს და დაიწყეს მისი მაგიურ სიმბოლოდ მიჩნევა და შელოცვებში გამოყენება. მაშასადამე, ახლა ნებისმიერ კვადრატულ ცხრილს, რომელიც შედგება რიცხვებისგან და აქვს ეს თვისება, ეწოდება ჯადოსნური კვადრატი.

რიცხვთა კვადრატს მაგია ეწოდება, თუ ყოველი ჰორიზონტალური მწკრივის, თითოეული ვერტიკალური მწკრივის და ორივე დიაგონალის ჯამები ერთნაირია. n რიგის რიცხვითი კვადრატი, სადაც n ნატურალური რიცხვია, არის კვადრატი დაყოფილი უჯრედებად, რომლებიც შეიცავს ბუნებრივ რიცხვებს 1-დან რა ჰქვია ჯადოსნურ კვადრატს?

K კვადრატების მიღება შესაძლებელია ლო შუდან კვადრატის ცენტრის ირგვლივ 90°, 180° ან 270°-ით მობრუნებით, ან მისი არეკვით. თუ უკვე ნაპოვნია რაიმე ჯადოსნური კვადრატი, მაშინ მისგან შეგიძლიათ გამოიყენოთ ზემოთ აღწერილი მეთოდები (ბრუნვა და სარკის ასახვა) კიდევ 7 ჯადოსნური კვადრატის მისაღებად. მიიღება ახალი ჯადოსნური კვადრატები: ტერასული მეთოდით, კვადრატული ჩარჩოს მეთოდით, დელერის მეთოდით, თუ ლათინური კვადრატის მეთოდით როგორ შედგება მაგიური კვადრატები?

ლო-შუ ჯადოსნური კვადრატის პოვნა შესაძლებელია 9 უჯრედში 9 ნომრის ყველა განლაგების გავლის გარეშე, ერთმანეთის მიყოლებით (ასეთი განლაგების რაოდენობაა 362,880). მოდით ვიფიქროთ ასე. 1-დან 9-მდე ყველა რიცხვის ჯამი უდრის: 1+2+3+4+5+6+7+8+9=45. ეს ნიშნავს, რომ თითოეულ მწკრივში და თითოეულ სვეტში რიცხვების ჯამი უნდა იყოს ტოლი: 45:3=15. მაგრამ თუ შეაჯამებთ ყველა რიცხვს მეორე სვეტში და მწკრივში და ორივე დიაგონალში, მაშინ თითოეული რიცხვი გამოჩნდება ერთხელ, გარდა ცენტრალურისა, რომელიც გამოჩნდება ოთხჯერ. ეს ნიშნავს, რომ თუ ცენტრალურ რიცხვს x-ით აღვნიშნავთ, მაშინ უნდა იყოს ტოლობა 4-15 = = 3x + 3-15. აქედან გამომდინარე, x=5, ანუ რიცხვი 5 უნდა იყოს ცხრილის ცენტრში. „ლო-შუ“ წესი.

მეოთხე რიგის ჯადოსნური კვადრატის დაწერა არ არის რთული: ამისათვის კვადრატში 1-დან 16-მდე რიცხვებს ვწერთ თანმიმდევრობით. ახლა მოდით შევცვალოთ რიცხვები მთელი კვადრატისა და შიდა კვადრატის საპირისპირო კუთხეებში: ვარდების ბურთის მეთოდი 1 5 2 3 7 9 10 11 6 13 4 16 12 8 14 15 16 13 4 1 11 10 7 6 16 253 9 4 14 15 1 8 12 11 10 7 6

ინსტრუქციები დიაგონალებით უკავშირდება არა მხოლოდ კვადრატის კუთხეები, არამედ მისი გვერდების შუაებიც, ანუ დიაგონალები დახატულია ოთხ 4x4 კუთხის კვადრატში (იხ. სურათი); იქნება რიცხვების თექვსმეტი ერთმანეთის სიმეტრიული წყვილი, რომლებიც უნდა შეიცვალოს: 1-64, 10-55, 19-46, 28-37, 8-57, 15-50, 22-43, 29-36, 4-61. , 5 -60, 11-54, 14-51, 18-47, 23-42, 25-40, 32-33. მერვე რიგის ჯადოსნური კვადრატის აგება ვარდების ბურთის მეთოდით

დაასრულეთ მერვე რიგის ჯადოსნური მოედანი, აგებული Rouse-Ball მეთოდით 1 2 2 3 3 4 4 5 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 23 23 25 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64

მათემატიკოსებმა გამოიგონეს ჯადოსნური კვადრატების აგების რამდენიმე მეთოდი.ჯადოსნური კვადრატის აგება ტერასული მეთოდით, რომელიც გამოიყენება უცნაური რიგის ჯადოსნური კვადრატების ასაგებად: მეხუთე, მეშვიდე და ა.შ. განვიხილოთ ეს მესამე რიგის ჯადოსნური კვადრატის მაგალითით. . ალგორითმი ტერასები ემატება თავდაპირველ 3x3 კვადრატს ოთხ მხარეს. მიღებულ ფიგურაში 1-დან 9-მდე რიცხვები განლაგებულია ბუნებრივი თანმიმდევრობით ირიბი რიგებით ქვემოდან ზევით. ტერასებზე რიცხვები, რომლებიც არ ხვდებიან კვადრატში, მოძრაობენ, თითქოს ტერასებთან ერთად, მის შიგნით ისე, რომ ისინი ერთვის კვადრატის მოპირდაპირე გვერდებს (რიცხვები, რომლებიც არ მოხვდება დაჩრდილულ კვადრატში, გადაინაცვლებს n = 3 ერთეულით. : 1 - ქვემოთ, 3 - მარცხნივ, 9 - ზემოთ, 7 - მარჯვნივ). მაშ ასე, განვიხილოთ ტერასების მეთოდი, კენტი რიგის ჯადოსნური კვადრატის შევსება, მაგალითად, მე-3 რიგის კვადრატების გამოყენებით. რიცხვებს ვწერთ შემდეგნაირად: რიცხვები, რომლებიც არ ხვდებიან დაჩრდილულ კვადრატში, გადაინაცვლებს n=3 ერთეულით: 1 – ქვემოთ, 3 – მარცხნივ, 9 – ზემოთ, 7 – მარჯვნივ. ჩვენ ვიღებთ ჯადოსნურ კვადრატს 3 3. რიცხვების ჯამი = 15. ტერასის მეთოდი 1 4 2 7 5 3 8 6 9 4 9 2 3 5 7 8 1 6

ახლა ჩვენ ავაშენებთ მეხუთე რიგის ჯადოსნურ კვადრატს ტერასის მეთოდით. კვადრატს შევავსებთ ეტაპობრივად, ალგორითმის მიხედვით. 1. ტერასები დაემატა თავდაპირველ 5x5 კვადრატს ოთხი მხრიდან. მიღებულ ფიგურაში ჩვენ ვაწყობთ რიცხვებს 1-დან 25-მდე ბუნებრივი თანმიმდევრობით ირიბი რიგებით ქვემოდან ზევით, როგორც მესამე რიგის კვადრატის მაგალითში. 2. რიცხვები, რომლებიც არ მოხვდება არჩეულ კვადრატში, გადაინაცვლებს n=5 ერთეულით: 1,2,6 – ქვემოთ, 4,5,10 – მარცხნივ, 24,25,20 – ზემოთ, 16,21,20 – უფლება. ვიღებთ: ჯადოსნური კვადრატის აგება n=5

Პრაქტიკული სამუშაო. 1 6 2 11 7 3 16 12 8 4 21 17 13 9 5 22 18 14 10 23 19 15 24 20 25 11 24 7 20 3 4 12 25 8 16 19 17 21 19 2 15

ტერასის მეთოდის გამოყენებით, თქვენ შეგიძლიათ ააწყოთ არა მხოლოდ უცნაური რიგის ტრადიციული ჯადოსნური კვადრატი, არამედ კვადრატი, რომელიც შევსებულია სხვა რიცხვებით, თუ განსხვავება ყოველ მომდევნო და წინა რიცხვს შორის მუდმივია. ასე რომ, სურათზე ხედავთ მეხუთე რიგის არატრადიციულ ჯადოსნურ კვადრატს, სავსე 2-დან 50-მდე ლუწი რიცხვებით, აგებული ტერასული მეთოდით.

6 32 18 44 30 40 16 42 28 4 14 50 26 2 38 48 24 10 36 12 22 8 34 20 46 სურათზე ხედავთ არატრადიციულ მეხუთე რიგის ჯადოსნურ კვადრატს, რომელიც აგებულია 2-დან 50-მდე ლუწი რიცხვებით. მეთოდი.

ლუწი-ლუწი რიგის ჯადოსნური კვადრატია n=4 m რიგის კვადრატი (m=1,2,3...), ანუ ასეთი კვადრატის რიგი იყოფა 4-ზე. ლუწი ჯადოსნური კვადრატებისთვის თუნდაც შეკვეთა, გამოიყენება კვადრატული ჩარჩო მეთოდი. ალგორითმი კვადრატული ჩარჩოები ორიგინალური კვადრატის მხარის ნახევრის გვერდით (იხ. ფიგურა) დახატულია მატრიცის ველზე (მასზე გამოსახულია ორიგინალური 8x8 კვადრატი) დიაგონალზე ერთი უჯრედის ნაბიჯით (ან ორი უჯრედი მწკრივში და სვეტები). შემდეგ რიცხვები 1-დან 2n-მდე მოთავსებულია ჩარჩოების ხაზების გასწვრივ, დაწყებული ორიგინალური კვადრატის ზედა მარცხენა კუთხიდან, პირველი ჩარჩო მიდის საათის ისრის მიმართულებით, მეორე ჩარჩო იწყება კვადრატის მარჯვენა ზედა თავისუფალი უჯრედიდან. და სვლა საათის ისრის საწინააღმდეგოდ და ა.შ. რიცხვები, რომლებიც არ ხვდება კვადრატში, გადაინაცვლებს მის შიგნით ისე, რომ ისინი ერთვის კვადრატის მოპირდაპირე მხარეს. დასრულებული ჯადოსნური კვადრატი ნაჩვენებია ნახ. კვადრატული ჩარჩო მეთოდი.

9 1 2 3 4 5 6 7 8 10 11 13 12 14 15 16 17 18 19 21 20 22 23 24 25 26 27 28 29 30 31 32 33

4 5 3 6 2 21 20 7 1 22 19 8 16 23 36 37 18 9 24 15 35 38 10 17 25 34 14 53 52 11 39 32 33 26 54 13 12 51 31 40 48 55 27 30 50 41 56 47 28 29 42 49 57 46 43 64 58 45 44 63 59 62 60 61

მზად არის 8-ბრძანების ჯადოსნური მოედანი

განმარტება. n რიგის განზოგადებული ლათინური კვადრატი არის n · n ზომის კვადრატული ცხრილი, რომლის ელემენტებს შორის მხოლოდ n ელემენტია გამორჩეული და n განსხვავებული ელემენტიდან რომელიმე ზუსტად n-ჯერ გვხვდება ამ ცხრილში. მშენებლობის მეთოდის აღწერა: ეტაპი 1. ჩვენ ვაშენებთ n რიგის განზოგადებულ ლათინურ კვადრატს შემდეგნაირად: კვადრატის ქვედა ნახევრის თითოეული ხაზი ივსება თანმიმდევრულად მონაცვლეობითი რიცხვებით i და n-i-1, სადაც i არის ხაზის სერიული ნომერი (ხაზები დანომრილია ქვემოდან ზემოდან. მთელი რიცხვებით 0-დან n-1-მდე); კვადრატის ზედა ნახევარი მიიღება ქვედა ნახევრიდან სიმეტრიის ვერტიკალურ ღერძთან ასახვით. ეტაპი 2. ჩვენ ვაშენებთ მეორე განზოგადებულ ლათინურ კვადრატს პირველიდან. ამისათვის თქვენ უნდა მოატრიალოთ პირველ ეტაპზე აგებული კვადრატი 90 გრადუსით საათის ისრის მიმართულებით. აღვნიშნავ, რომ ამ გზით მიღებული ორი ლათინური კვადრატი ორთოგონალური იქნება, მაგრამ ორთოგონალური ლათინური კვადრატების განმარტება არ მიმიცია, რადგან ამას არ აქვს მნიშვნელობა წარმოდგენილი მშენებლობის მეთოდის გასაგებად. ეტაპი 3. ჩვენ ვაშენებთ სრულყოფილ კვადრატს შემდეგნაირად. პირველი ლათინური კვადრატის ელემენტები ავღნიშნოთ მეორე ლათინური კვადრატის ელემენტებად - მაშინ სრულყოფილი კვადრატის თითოეული შესაბამისი ელემენტი მიიღება ფორმულით: n + + 1 ჯადოსნური კვადრატის აგება დელერის მეთოდით ან მეთოდით. ლათინური კვადრატები.

პირველი მეორე ჯადოსნური ლათინური კვადრატი მეოთხე რიგის ლათინური კვადრატული კვადრატი 2 1 2 1 1 3 0 3 0 1 2 1 2 0 3 0 3 0 1 3 2 3 2 0 1 0 1 3 2 3 2 0 1 9 6 12 7 16 3 13 2 5 10 8 11 4 15 1 14 კვადრატის ბოლოსთვის: პირველი ხაზი: i = 0, 4-i- 1= 4-0-1=3. რიცხვები 0 და 3 ალტერნატიული მეორე ხაზი: i =2, 4-2-1=1. რიცხვები 2 და 1 ალტერნატიულია. კვადრატის ზედა ნაწილისთვის ჩვენ სიმეტრიულად ასახავს ქვედა ნაწილის ნომრებს (ისრების გასწვრივ). i = 3 i = 2 i = 1 i = 0 მიღებულია პირველი კვადრატიდან საათის ისრის მიმართულებით 90°-ით ბრუნვით. მივიღეთ ფორმულის გამოყენებით =2·4+0+1=9 = 1·4+1+1=6 = 2·4+3+1=12 = 1·4+2+1=7 = 3·4 +3+ 1=16 = 0·4+2+1=3 = 3·4+0+1=13 და ასე შემდეგ 1 2 3 4 1 2 3 4

ჯადოსნური მოედნების გაჩენა უძველესი დროიდან თარიღდება. მათ შესახებ ყველაზე ადრეული ინფორმაცია, როგორც ჩანს, შეიცავს IV-V საუკუნეებში დაწერილ ჩინურ წიგნებში. ძვ.წ ე. ჩვენამდე მოღწეული უძველესი ჯადოსნური კვადრატებიდან „უძველესი“ არის ლო-შუს მაგიდა (ძვ. წ. 2200 წ.). შემდეგი უახლესი ინფორმაცია ჯადოსნური კვადრატების შესახებ ჩვენთან მოვიდა ინდოეთიდან და ბიზანტიიდან. ევროპაში ჯადოსნური კვადრატების გამოსახულება პირველად გვხვდება გერმანელი მხატვრის ალბრეხტ დიურერის გრავირებაში "მელანქოლია" (1514). ეს ჯადოსნური კვადრატი შედგება 16 უჯრედისაგან: 4 მწკრივი და 4 სვეტი, სავსეა 1-დან 16-მდე ნატურალური რიცხვებით. მასში თითოეული მწკრივის, თითოეული სვეტის და ორი დიაგონალის რიცხვების ჯამი არის 34. ქვედა მწკრივის შუა რიცხვები. (15 და 14) ნიშნავს თარიღი 1514 არის გამოქვეყნების წელი ამ გრავიურა A. Durer. ბევრი მათემატიკოსი სწავლობდა ჯადოსნური კვადრატების შედგენის მეთოდებს: მე-16 საუკუნეში. A. Riese და M. Stiefel, XVII საუკუნეში. ა.კირხერი და ბაშე დე მესერიაკი. ჯადოსნური კვადრატების თეორია შეისწავლა ფრანგმა მათემატიკოსმა დელერმა. ლეონჰარდ ეილერმა მოიფიქრა ჭადრაკის რაინდის მეთოდი რამდენიმე ჯადოსნური კვადრატის ასაგებად. ჯადოსნური კვადრატების თეორია არანაირად არ შეიძლება ჩაითვალოს დასრულებულად. ყველა ჯადოსნური კვადრატის აგების ზოგადი მეთოდი ჯერ კიდევ უცნობია და მათი რაოდენობა უცნობია.

მათემატიკური ტერმინების განმარტებითი ლექსიკონი. ო.ვ. Ya. V. Uspensky შერჩეული მათემატიკური გასართობი. - Sower, 1924. B. A. Kordemsky მათემატიკური გამომგონებლობა. - M.: GIFML, 1958. - 576გვ. M. M. Postnikov ჯადოსნური კვადრატები. - M.: Nauka, 1964. N. M. Rudin ჯადოსნური მოედნიდან ჭადრაკამდე. - M.: ფიზიკური კულტურა და სპორტი, 1969. E. Ya. Gurevich უძველესი ტალიმენის საიდუმლო. - M.: Nauka, 1969. M. Gardner მათემატიკური დასვენება. - მ.: მირი, 1972. ახალგაზრდა მათემატიკოსის ენციკლოპედიური ლექსიკონი. - M.: პედაგოგიკა, 1989. Yu. V. Chebrakov Magic Squares. რიცხვთა თეორია, ალგებრა, კომბინატორული ანალიზი. - სანკტ-პეტერბურგი: პეტერბურგის შტატი. ტექ. უნივ., 1995. იუ.ვ.ჩებრაკოვის მაგიური მატრიცების თეორია. - სანკტ-პეტერბურგი, 2008. მ. გარდნერი თავი 17. ჯადოსნური კვადრატები და კუბები // დროში მოგზაურობა. - მ.: მირი, 1990. საჭადრაკო მიდგომა ლიტერატურა

პრეზენტაციის აღწერა ინდივიდუალური სლაიდებით:

1 სლაიდი

სლაიდის აღწერა:

ჯადოსნური კვადრატების საიდუმლოებები. ნაწარმოების ავტორი: იუნევა ელიზავეტა ალექსანდროვნა სამუშაო ადგილი: სოფელი სოლდატო-ალექსანდროვსკოე, მუნიციპალური საგანმანათლებლო დაწესებულება "სოლდატო-ალექსანდროვსკოეს მე-6 საშუალო სკოლა", მე-6 კლასი "ა" სამეცნიერო ხელმძღვანელი: დენისოვა ნატალია ვალერიევნა, მუნიციპალური მათემატიკის მასწავლებელი. "სოლდატო-ალექსანდროვსკოეს მე-6 საშუალო სკოლა"

2 სლაიდი

სლაიდის აღწერა:

შესავალი "ჯადოსნური კვადრატების დამზადება შესანიშნავი გონებრივი ტანვარჯიშია განლაგების, კომბინაციისა და სიმეტრიის იდეების გაგების უნარის გასავითარებლად." ლეონარდ ეილერი ჯადოსნური კვადრატები... ეს ფრაზა მაშინვე მაგიის სუნი ასდის. ანტიკურობის დიდი მეცნიერები სამყაროს არსის საფუძვლად რაოდენობრივ ურთიერთობებს თვლიდნენ. მათ დაინახეს, რომ ციფრებს აქვთ გარკვეული დამოუკიდებელი ცხოვრება, საკუთარი საიდუმლოებები. მოგვიანებით გაირკვა, რომ რიცხვების სწორ რიგებში დალაგებით, „ჯადოსნობის“ შემთხვევაში შეგიძლიათ დაამატოთ ისინი მარცხნიდან მარჯვნივ და ზემოდან ქვემოდან, ყოველ ჯერზე, როდესაც მიიღებთ თანაბარ რიცხვებს. ამრიგად, დროთა განმავლობაში ჩამოყალიბდა ჯადოსნური მოედანი, რომელსაც დღემდე ვხედავთ.

3 სლაიდი

სლაიდის აღწერა:

პროექტის მიზანი: ჯადოსნური კვადრატების შევსების გზების და მათი გარეგნობის ისტორიის შესწავლა; გაარკვიეთ ჯადოსნური კვადრატების შექმნის სხვადასხვა გზები; შეისწავლეთ მათი გამოყენების სფეროები. პროექტის მიზნები: 1. გაეცნონ ჯადოსნური კვადრატების გარეგნობის ისტორიას და სახელწოდებებს; 2.ჯადოსნური კვადრატების შევსების ცნობილი მეთოდების შესწავლა; 3. გაარკვიეთ ჯადოსნური კვადრატის გამოყენების სფეროები. კვლევის თემა: ჯადოსნური კვადრატების შევსება; კვლევის ობიექტი: ჯადოსნური კვადრატი; ჰიპოთეზა: ჯადოსნური კვადრატის შესავსებად, არსებობს სპეციალური ტექნიკა, რომელიც საშუალებას გაძლევთ ამის გაკეთება სწრაფად

4 სლაიდი

სლაიდის აღწერა:

მუშაობისას გამოყენებული იქნა შემდეგი მეთოდები: ძიების მეთოდი (საცნობარო და საგანმანათლებლო ლიტერატურის, ასევე გლობალური ინტერნეტის საინფორმაციო რესურსების გამოყენება); პრაქტიკული მეთოდი (შეძენილი ცოდნის საფუძველზე ჯადოსნური კვადრატების დახატვა); კვლევის მეთოდი (პიროვნების ფსიქოლოგიური პორტრეტის დახატვა პითაგორას კვადრატის გამოყენებით).

5 სლაიდი

სლაიდის აღწერა:

ჯადოსნური კვადრატის გარეგნობის ისტორია ჯადოსნური მოედანი უძველესი ჩინური წარმოშობისაა. ლეგენდის თანახმად, იმპერატორ იუ-ს (ძვ. წ. 2200 წ.) მეფობის დროს ყვითელი მდინარის (ყვითელი მდინარის) წყლიდან ამოვიდა წმინდა კუ, რომლის გარსზე იდუმალი იეროგლიფები იყო დატანილი და ეს ნიშნები ცნობილია როგორც ლუ-შუ. და ჯადოსნური კვადრატის ტოლფასია. მე-11 საუკუნეში მათ გაიგეს ჯადოსნური მოედნების შესახებ ინდოეთში, შემდეგ კი იაპონიაში, მე-15 საუკუნეში. ევროპელებმა გაიგეს ჯადოსნური მოედნების შესახებ. ევროპელის მიერ გამოგონებულ პირველ კვადრატად ითვლება დიურერის მოედანი, რომელიც გამოსახულია მის ცნობილ გრავირებაში „მელანქოლია 1“. გრავიურის შექმნის თარიღი (1514 წ.) მითითებულია ქვედა ხაზის ორ ცენტრალურ უჯრაში. სხვადასხვა მისტიკურ თვისებებს მიაწერდნენ მაგიურ კვადრატებს. ითვლებოდა, რომ ვერცხლზე ამოტვიფრული ჯადოსნური კვადრატი იცავდა ჭირისგან. დღესაც კი, ევროპელი მჭევრმეტყველების ატრიბუტებს შორის შეგიძლიათ ნახოთ ჯადოსნური კვადრატები. მე-19 და მე-20 საუკუნეებში. ინტერესი ჯადოსნური კვადრატებისადმი განახლებული ენერგიით გაიზარდა. მათ შესწავლა დაიწყეს უმაღლესი ალგებრის მეთოდების გამოყენებით.

6 სლაიდი

სლაიდის აღწერა:

MAGIC SQUARE არის მთელი რიცხვების კვადრატული ცხრილი, რომელშიც რიცხვების ჯამები ნებისმიერი მწკრივის, ნებისმიერი სვეტის და ორი ძირითადი დიაგონალიდან ერთნაირი რიცხვის ტოლია. სახელწოდება "ჯადოსნური" მოედნები მოვიდა არაბებისგან, რომლებმაც დაინახეს რაღაც მისტიური მათ თვისებებში და ამიტომ მიიღეს კვადრატები, როგორც უნიკალური თილისმანები, რომლებიც იცავდნენ მათ, ვინც მათ ეცვათ მრავალი უბედურებისგან. შუა საუკუნეების არაბმა მათემატიკოსებმა ასევე გამოიჩინეს ინტერესი საოცარი კვადრატების მიმართ და მოიხსენიეს მათი მაგალითები თავიანთ ნაწერებში. სხვადასხვა მისტიკურ თვისებებს მიაწერდნენ ჯადოსნურ კვადრატებს, თითქოს მათ შეეძლოთ ადამიანის განკურნებაც კი საშინელი დაავადებებისგან. ჯადოსნური კვადრატების დამზადება მათემატიკოსებში პოპულარული გატარება იყო და იქმნებოდა უზარმაზარი კვადრატები. თუ კვადრატში რიცხვების ჯამები მხოლოდ მწკრივებში და სვეტებში ტოლია, მაშინ მას ნახევრად მაგია ეწოდება.

7 სლაიდი

სლაიდის აღწერა:

ჯადოსნური კვადრატების გამოყენება როცა გადავხედე ჯადოსნური კვადრატების შედგენის მეთოდებს, დავინტერესდი მათი გამოყენების ფარგლებით. ის საკმაოდ საინტერესო მეჩვენა. ძალიან პოპულარულია იაპონური თავსატეხი სუდოკუ, რომლის წინაპარად შეიძლება ჩაითვალოს ჯადოსნური მოედანი. ის გვეხმარება ლოგიკური აზროვნების და გამოთვლითი უნარების განვითარებაში. დღესდღეობით ბევრი გაზეთი აქვეყნებს ამ თავსატეხებს კროსვორდებთან და სხვა ლოგიკურ პრობლემებთან ერთად. კარგად, და, რა თქმა უნდა, ნუმეროლოგიაში. დიდი მეცნიერი პითაგორაც კი თვლიდა, რომ მსოფლიოში ყველაფერი აკონტროლებს რიცხვებს. მაშასადამე, ადამიანის არსი რიცხვშიც მდგომარეობს - მისი დაბადების თარიღი. მან შექმნა კვადრატის აგების მეთოდი, რომლითაც შეიძლება გაიგოს ადამიანის ხასიათი, მისი ჯანმრთელობის მდგომარეობა და მისი პოტენციალი, გამოავლინოს მისი ძლიერი და სუსტი მხარეები და ამით დაადგინოს რა უნდა გაკეთდეს მის გასაუმჯობესებლად. პითაგორას დროს ჯადოსნური კვადრატები ინდივიდუალურად იქმნებოდა თითოეული ადამიანისთვის. ახლა არის სპეციალური პროგრამა, სადაც შეყვანილია ადამიანის დაბადების თარიღი და ეკრანზე გამოსახულია მზა ჯადოსნური კვადრატი. მე გავაკეთებ ჯადოსნურ კვადრატს ჩემთვის.

8 სლაიდი

სლაიდის აღწერა:

დავიბადე 2004 წლის 10 ნოემბერს. ვამატებთ დაბადების თვის და წლის რიცხვებს, ვიღებთ პირველ სამუშაო რიცხვს 9. შემდეგ ვამატებთ პირველი სამუშაო რიცხვის ციფრებს და ვიღებთ მეორე სამუშაო რიცხვს 9. პირველ სამუშაო რიცხვს გამოვაკლებთ დაბადების დღის პირველ ციფრს ორჯერ, ასე რომ მივიღებთ მესამე სამუშაო რიცხვს: 9-2=7. მესამე სამუშაო რიცხვის ციფრების ჯამიდან ვიღებთ მეოთხე სამუშაო რიცხვს: 7 დავხატოთ 3-ზე 3-ზე კვადრატი, ჩვენი ორი წრფედან ვითვლით რიცხვებში ერთეულთა რაოდენობას - ვწერთ პირველ კვადრატში. მეორე უჯრედი შეიცავს ორს, მესამე - სამს და ა.შ. "111" - დადებითი პიროვნება, სტაბილური ხასიათი. "2" - მე ვარ მგრძნობიარე ადამიანი ატმოსფეროში ცვლილებების მიმართ, "4" - მაქვს შესანიშნავი ჯანმრთელობა, "77" - მაქვს ყველაფერი - კარგი და ცუდი. გემოვნება მაქვს, კარგად ვხატავ, ძალიან ნიჭიერი ვარ. უსიამოვნების შემთხვევაში შემიძლია თავი დავაღწიო. "99" დაბადებიდან ჭკვიანია, ცოდნა ადვილად მოდის. 111 4 77 2 - - - - 99

სლაიდი 9

სლაიდის აღწერა:

ჯადოსნური კვადრატების გამოყენების კიდევ ერთი ტრადიციული სფეროა ტალიმანები. მაგალითად, მთვარის თილისმას აქვს გარკვეული თვისებები: ის იცავს გემის ჩაძირვისა და ავადმყოფობისგან, აქცევს ადამიანს კეთილგანწყობილს, ხელს უწყობს ცუდი ზრახვების თავიდან აცილებას და ასევე აუმჯობესებს ჯანმრთელობას. იგი ვერცხლზეა ამოტვიფრული მთვარის დღესა და საათზე, როცა მზე ან მთვარე კირჩხიბის პირველ ათ გრადუსზეა. მე-9 რიგის ჯადოსნური კვადრატი ჯდება ექვსკუთხედში (9 არის მთვარის რიცხვი) და გარშემორტყმულია სპეციალური სიმბოლოებით.

10 სლაიდი

სლაიდის აღწერა:

ჯადოსნური კვადრატების ტიპები არ არსებობს 2*2 ჯადოსნური კვადრატები. 2*2 ზომის კვადრატი უნდა შედგებოდეს 1,2,3,4 რიცხვებისგან და მისი მუდმივი იყოს 5. ასეთ კვადრატს ექნება ორი მწკრივი, სვეტი და დიაგონალები. იმისათვის, რომ კვადრატი გახდეს ჯადოსნური, თქვენ უნდა წარმოადგინოთ რიცხვი 5, როგორც ორი მოცემული რიცხვის ჯამი ექვსი განსხვავებული გზით, მაგრამ ეს შეუძლებელია! ყოველივე ამის შემდეგ, არსებობს მხოლოდ ორი ასეთი კომბინაცია: 1+ 4 და 2+3. არსებობს მხოლოდ ერთი 3*3 ჯადოსნური კვადრატი, რადგან დარჩენილი 3*3 ჯადოსნური კვადრატები მიიღება მისგან ან რიგების ან სვეტების გადალაგებით, ან თავდაპირველი კვადრატის 90 ან 180 გრადუსით შებრუნებით.

11 სლაიდი

სლაიდის აღწერა:

3x3 ჯადოსნური კვადრატის შედგენის ალგორითმი 1) ჩაწერეთ რიცხვები სურათზე ნაჩვენები თანმიმდევრობით: 1 2 3 4 5 6 7 8 9 2) შეცვალეთ რიცხვები დიაგონალების საპირისპირო ბოლოებზე: 1 და 9, 3 და 7: 9 2 7 4 5 6 3 8 1 3) გადაიტანეთ თითოეული რიცხვი ერთი ნაბიჯით საათის ისრის მიმართულებით 4 9 2 3 5 7 8 1 6 ამრიგად, მივიღებთ ჯადოსნურ კვადრატს, რომლის ჯადოსნური ჯამი (ე.ი. რიცხვების ჯამი ნებისმიერში ხაზი, ნებისმიერ სვეტში და თითოეულ დიაგონალზე) უდრის 15-ს. მიმართულებას მნიშვნელობა არ აქვს, მთავარია შევინარჩუნოთ რიცხვების რიგი.

12 სლაიდი

სლაიდის აღწერა:

ლო-შუს მოედანი. პირველი 9 ბუნებრივი რიცხვის მე-3 რიგის ჯადოსნური კვადრატი (ჩინეთში ცნობილია როგორც ლუო შუ ტალიმენი) წარმოდგენილია 3x3 მატრიცით. კვადრატების აგების ზოგადი მეთოდი უცნობია. ჯადოსნური კვადრატების აგების წესები დაყოფილია სამ კატეგორიად, კვადრატის რიგის მიხედვით. კვადრატები შეიძლება იყოს: - კენტი, ანუ შედგება კენტი რაოდენობის უჯრედებისაგან, - ლუწი-ლუწი, ანუ რიგი უდრის ორჯერ ლუწი; - ლუწი-კენტი, ანუ რიგი უდრის ორჯერ კენტს.

სლაიდი 13

სლაიდის აღწერა:

მეოთხე რიგის კვადრატი. 4x4 ჯადოსნური კვადრატი გამოსახული ალბრეხტ დიურერის გრავიურაზე „მელანქოლია I“ ითვლება ყველაზე ადრეულ ევროპულ ხელოვნებაში. ქვედა რიგში ორი შუა რიცხვი მიუთითებს ნახატის შექმნის თარიღზე (1514 წ.). რიცხვების ჯამი ნებისმიერ ჰორიზონტალურ, ვერტიკალურ და დიაგონალზე არის 34. ეს ჯამი ასევე გვხვდება ყველა 2x2 კუთხის კვადრატში, ცენტრალურ მოედანზე (10+11+6+7), კუთხის უჯრების კვადრატში (16+13+). 4+1 ), „რაინდის სვლით“ აგებულ კვადრატებში (2+8+9+15 და 3+5+12+14), მართკუთხედებში, რომლებიც წარმოიქმნება საპირისპირო მხარეს შუა უჯრედების წყვილით (3+2+15+). 14 და 5+8 +9+12).

სლაიდი 14

სლაიდის აღწერა:

ეშმაკის ჯადოსნური მოედანი. ეშმაკის ჯადოსნური კვადრატი არის ჯადოსნური კვადრატი, რომელშიც ორივე მიმართულებით გატეხილი დიაგონალის გასწვრივ რიცხვების ჯამები ასევე ემთხვევა მაგიურ მუდმივას. ასეთ კვადრატებს ასევე უწოდებენ პანდიაგონალს. არის 48 4x4 ეშმაკის ჯადოსნური კვადრატი ბრუნვისა და ასახვის სიზუსტით. მეოთხე რიგის პანდიაგონალურ კვადრატებს აქვთ მრავალი დამატებითი თვისება, რისთვისაც მათ სრულყოფილს უწოდებენ. არ არსებობს უცნაური რიგის სრულყოფილი კვადრატები.

MBOU "ვოჟეგოდსკაია SS"

ჯადოსნური მოედანი

მათემატიკის კლუბის გაკვეთილი მე-5 კლასში

სამუშაოს მიზანი:

გაეცანით ჯადოსნურ კვადრატებს.

1. გაეცანით კვადრატების გარეგნობის ისტორიას.

2. გამოიკვლიეთ კვადრატების თვისებები.

3. გაეცანით კვადრატების შევსების წესებს.

3. ისწავლეთ 3-ზე 3 ჯადოსნური კვადრატის სწორად და სწრაფად შევსება.

ჩამოყალიბდა UUD

შემეცნებითი:დაამტკიცეთ, გამოიტანეთ დასკვნები, ააგეთ ლოგიკურად გამართული მსჯელობა.

მარეგულირებელი:განსაზღვროს მიზანი, აქტივობის პრობლემა; წამოაყენე ვერსიები; თვითკონტროლი და კორექტირება.

კომუნიკაბელური:გამოხატეთ თქვენი აზრი, მოაწყვეთ მუშაობა წყვილებში (დასვით კითხვები, შეიმუშავეთ გამოსავალი).

პირადი:თანაკლასელების მიმართ პატივისცემით განწყობილი, ახალი ცოდნის შეძენის აუცილებლობის გაცნობიერება.

გაკვეთილის მიმდინარეობა

1. დაფაზე დაწერილი ცნებებიდან რომელი ვიცით:

- მათემატიკური სოფისტიკა(მტკიცებულება შეცდომით მოიძებნება)

- მათემატიკური პარადოქსი(განცხადება, რომელიც შეიძლება ჩაითვალოს როგორც ჭეშმარიტად, ასევე მცდარი)

- მობიუსის ზოლები(ტოპოლოგიური ფიგურა, რომელსაც აქვს ერთი უსასრულო მხარე)

- ჯადოსნური მოედანი

ჩვენი გაკვეთილის თემაა "ჯადოსნური მოედანი"

დავიწყებ ლეგენდით, რომლის მიხედვითაც ჩინეთის იმპერატორმა იიუმ, რომელიც ცხოვრობდა ოთხი ათასი წლის წინ, ერთხელ მდინარის ნაპირზე დაინახა წმინდა კუ, რომლის ნაჭუჭზე შავი და თეთრი წრეების ნიმუში იყო. სწრაფმა იმპერატორმა მაშინვე მიხვდა ამ ნახატის მნიშვნელობა. შეეცადეთ ასევე განსაზღვროთ.

იპოვეთ რიცხვების ჯამი, რომლებიც წარმოდგენილია წრეებით თითოეულ მწკრივში, სვეტში და დიაგონალში

თითოეული მწკრივის, სვეტისა და დიაგონალის რიცხვების ჯამი არის 15.

სწორედ ამ კვადრატს მათემატიკაში ჰქვია მაგია. ჯადოსნური კვადრატების თვისებები ჯადოსნურად ითვლებოდა როგორც ძველ ჩინეთში, ასევე შუა საუკუნეების ევროპაში. ჯადოსნური კვადრატები ემსახურებოდა თილისმანებს, იცავდა მათ, ვინც მათ ატარებდა სხვადასხვა პრობლემებისგან.

გერმანელი მხატვრის ალბრეხტ დიურერის გრავიურაზე „მელანქოლია“ (1514) ასევე გამოსახულია კვადრატი. დაამტკიცეთ, რომ ეს ჯადოსნურია.

თითოეული მწკრივის, სვეტის და დიაგონალის ციფრების ჯამი არის 34.

ამ მოედანზე სხვა საინტერესო თვისებებია. იპოვეთ რიცხვების ჯამი 2-ზე 2 კვადრატში, ყველა კუთხის უჯრედში.

ახლა კი, როცა ცოტა რამ გავიგეთ რა არის ჯადოსნური კვადრატი, შეეცადეთ ჩამოაყალიბოთ ჩვენი გაკვეთილის მიზანი. (ისწავლეთ შევსება). Დავალებები? (ისწავლეთ წესი, ივარჯიშეთ).

როგორ გააკეთოთ ჯადოსნური კვადრატი?

კვადრატის ერთი მხარის გასწვრივ უჯრედების რაოდენობა აღინიშნება ასო n-ით და ეწოდება კვადრატის რიგი. არის ნებისმიერი რიგის კვადრატი მე-2-ის გარდა. უმარტივესი (ტრივიალური) არის 1 რიგის კვადრატი, რომელიც შედგება ერთი უჯრედისგან. უმარტივესი ჯადოსნური კვადრატები ერგება ნატურალურ რიცხვებს 1-დან n2 + 1-მდე

რიცხვების ჯამი თითოეულ რიგში, თითოეულ სვეტში და ჯადოსნური კვადრატის ნებისმიერ დიაგონალზე მაგიური მუდმივი ეწოდება მ. ჯადოსნური მუდმივი n განისაზღვრება ფორმულით:

იპოვეთ ჯადოსნური მუდმივი მე-3 რიგის კვადრატისთვის (15), მე-4 რიგის (34), მე-5 რიგის (65).

ჩვენ დავიწყებთ უმარტივესი მესამე რიგის ჯადოსნური კვადრატის აგებით. ჩვენ ვიცით, რომ ჰორიზონტალურად, ვერტიკალურად და დიაგონალზე ყველა რიცხვის ჯამი არის 15. შეადგინეთ რიცხვების სამეულის ყველა შესაძლო ჯამი 1-დან 9-მდე, რომლებიც მიიღებენ 15-ს.

რომელი რიცხვი ჩნდება ყველაზე ხშირად? (5 - 4 ჯერ) ეს ნიშნავს, რომ რიცხვი 5 უნდა იყოს ცხრილის 4 მწკრივის გადაკვეთაზე. სად უნდა იყოს? (მაგიდის ცენტრში). დარჩენილი ნომრები თავად გაანაწილეთ.

რა კვადრატები მიიღეთ?

თუ მართკუთხა ჩარჩოს გარშემო შემოახვევთ 4x4 „ჯადოსნურ“ კვადრატს, შეგიძლიათ აღმოაჩინოთ მრავალი სხვა თვისება.

ჩარჩოს გარშემო ოთხი რიცხვის ჯამი ნებისმიერი მიმართულებით არის 34

ოთხი რიცხვის ჯამი, რომლებიც გვხვდება თითოეულ კუთხეში გარედან და თითოეულ კუთხეში შიგნით არის ასევე 34

ერთი და იმავე ფერის ოთხი რიცხვის ჯამი არის 34

თუ თქვენ დაამატებთ რიცხვებს სპირალურად საათის ისრის მიმართულებით ან საათის ისრის საწინააღმდეგოდ, ჩარჩოს გარშემო, დაწყებული სადმე - 34.

შევაჯამოთ. მივაღწიეთ თუ არა ჩვენს მიზანს?

რესურსების წრე. რა ახალი რამ ისწავლეთ, თქვენი შთაბეჭდილებები გაკვეთილზე. ტეტრაედონი ერთმანეთს გადავეცით – ამ გეომეტრიულ სხეულსაც არაჩვეულებრივი თვისებები აქვს. და ჩვენ გავარკვევთ, როგორები არიან ისინი კლუბის ერთ-ერთ კლასში.

დარიგება

ჯადოსნური მოედანი

n - კვადრატული წესრიგი

ჯადოსნური მოედანი, ნ = 3

ჯადოსნური მოედანი

n - კვადრატული წესრიგი

M - კვადრატის ჯადოსნური მუდმივი

ჯადოსნური მოედანი, ნ = 3

9 = 1 + 5 + 9, 9 = ______________, 9 = ______________,

9 = 2 + 5 + 8, 9 = ______________, 9 = ______________,

9 = ______________, 9 = ______________.

...მათემატიკური ჭეშმარიტებები უკვდავია, არ ექვემდებარება გახრწნას და იგივე რჩება გუშინ, დღეს და სამუდამოდ.

ერიკ ტემპლ ბელი (1883-1960)

კემეროვოს რეგიონის განათლებისა და მეცნიერების დეპარტამენტი

სახელმწიფო საბიუჯეტო საგანმანათლებლო დაწესებულება

საშუალო პროფესიული განათლება

"ნოვოკუზნეცკის ტრანსპორტისა და ტექნოლოგიების კოლეჯი"

ჯადოსნური კვადრატები (ზეპირი ჟურნალი)

ნაიმუშინა კრისტინა ანდრეევნა,

მელკოვი მაქსიმ სერგეევიჩი

"Ისტორიული"

1 გვერდი

ჯადოსნური კვადრატები დიდ პატივს სცემდნენ და მათ სხვადასხვა მისტიკურ თვისებებს მიაწერდნენ. .

"შემეცნებითი"

2 გვერდი

ჯადოსნური ან ჯადოსნური კვადრატი არის კვადრატული ცხრილი, რომელიც ივსება რიცხვებით ისე, რომ თითოეულ მწკრივში, თითოეულ სვეტში და ორივე დიაგონალზე რიცხვების ჯამი ერთნაირია. თუ კვადრატში რიცხვების ჯამები მხოლოდ მწკრივებში და სვეტებში ტოლია, მაშინ მას ნახევრად მაგია ეწოდება. . ნორმალური კვადრატი არის ჯადოსნური კვადრატი, რომელიც სავსეა 1-დან დაწყებული მთელი რიცხვებით.

შევსებული ჯადოსნური კვადრატიდან შეგიძლიათ მიიღოთ ახალი ჯადოსნური კვადრატი კვადრატის ყველა რიცხვის იმავე რიცხვით გაზრდით

მ =15

მ =21

შევსებული ჯადოსნური კვადრატიდან ახალი ჯადოსნური კვადრატის მიღება შესაძლებელია სიმეტრიის ღერძების მიმართ ასახვით.

შევსებული ჯადოსნური კვადრატი შეიძლება გამოყენებულ იქნას ახალი ჯადოსნური კვადრატის შესაქმნელად. ცენტრის გარშემო შემობრუნება

"პრაქტიკული"

3 გვერდი

კენტი კვადრატები

ვაშენებთ კვადრატულ ABCD-ს 25 უჯრედით და დროებით ვაფართოვებთ მას სიმეტრიულ საფეხურ ფიგურამდე ერთი უჯრედის საფეხურებით.
მიღებულ ფიგურაში ვათავსებთ 25 მთელ რიცხვს 1-დან 25-მდე, ზემოდან ქვემოდან - მარჯვნივ ირიბი რიგების მიხედვით.
ახლა კი თითოეული რიცხვი, რომელიც არის ABCD კვადრატის გარეთ, უნდა გადავიდეს იმავე მწკრივის ან სვეტის გასწვრივ იმ უჯრიდან, რომელსაც ის იკავებს, რა არის კვადრატის რიგი, ჩვენს მაგალითში - ხუთი. მაშ ასე, ამ წესის შესაბამისად, ჩვენ გადავცემთ ამ ნომრებს...

კვადრატები შეკვეთა, ოთხის მრავალჯერადი

განათავსეთ რიცხვები მოცემული კვადრატის უჯრებში აღმავალი მიმდევრობით (ბუნებრივი თანმიმდევრობით).
აირჩიეთ ოთხი კვადრატი n/4 გვერდით მოცემული კვადრატის კუთხეებში და ერთი კვადრატი n/2 გვერდით ცენტრში.
შერჩეულ ხუთ კვადრატში შეცვალეთ რიცხვები, რომლებიც სიმეტრიულად მდებარეობს მოცემული კვადრატის ცენტრთან მიმართებაში.
მითითებული ნიმუშის მიხედვით შედგენილი კვადრატები ყოველთვის იქნება ჯადოსნურად სიმეტრიული.

"Კვლევა"

4 გვერდი

თილისმანები მთვარის ტალიმენი

მონაცემთა დაცვა ტექსტის დაშიფვრა

O I R M E O S Y V T A L G O P

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

ჩამოსვლა

სუდოკუარის რიცხვების თავსატეხი, რომელიც ბოლო დროს ძალიან პოპულარული გახდა. იაპონურიდან თარგმნილი, "su" ნიშნავს "რიცხვს" და "doku" ნიშნავს "მარტო დგომას".

ექსპერიმენტები სოფლის მეურნეობაში, ფიზიკაში, ქიმიაში, ტექნოლოგიაში.

ხორბლის 4 ჯიშის მოსავლიანობის ტესტირება

"გასართობი"

5 გვერდი

ადამიანის ხასიათის გაგება:

პითაგორას მოედანი

პრეზენტაცია მოამზადა კუზნეცოვმა ა, 9ა კლასი, 27-ე სკოლა

სლაიდი 2: 1

ჯადოსნური კვადრატი არის კვადრატი, რომელიც შედგება n სვეტისა და n მწკრივისაგან, რომელთა თითოეულ უჯრედში იწერება რიცხვი. კვადრატში რიცხვები მოთავსებულია ისე, რომ ყოველი ჰორიზონტალური, ვერტიკალური და დიაგონალური მწკრივი იძლევა ერთსა და იმავე ჯამს.

სლაიდი 3

მსოფლიოში უძველესი ჯადოსნური მოედანი ნაჩვენებია ზემოთ. შავი წრეები ამ კვადრატში წარმოადგენს ლუწ (ქალის) რიცხვებს, ხოლო თეთრი წრეები კენტ (მამაკაცურ) რიცხვებს. ნორმალურ ჩაწერაში ეს არც ისე ეფექტურია: 6 1 8 7 5 3 2 9 4

სლაიდი 4: ჯადოსნური კვადრატი მე-5 რიგი

დადასტურებულია, რომ მე-5 რიგის 13 მილიონზე მეტი ჯადოსნური კვადრატია მე-5 რიგის ჯადოსნური კვადრატი.

სლაიდი 5: პითაგორას ჯადოსნური მოედანი

პითაგორამ შექმნა კვადრატის აგების მეთოდი, რომლითაც შეიძლება გაიგოს ადამიანის ხასიათი, მისი ჯანმრთელობის მდგომარეობა და მისი პოტენციალი და გამოავლინოს მისი ძლიერი და სუსტი მხარეები.

სლაიდი 6: დიურერის ჯადოსნური მოედანი

მის ზედა მარჯვენა კუთხეში არის მე-4 რიგის ჯადოსნური კვადრატი. თითოეულ რიგში რიცხვების ჯამი არის 34. დიურერის ჯადოსნური კვადრატი

სლაიდი 7: ა. დიურერის ჯადოსნური კვადრატის თვისებები

ევროპაში ჯადოსნური მოედნები მხოლოდ მე-15 საუკუნის დასაწყისში შეაღწიეს. ხოლო XVI საუკუნის დასაწყისში, ერთ-ერთი მათგანი უკვდავყო გამოჩენილმა გერმანელმა მხატვარმა, გრავირმა და გარკვეულწილად მათემატიკოსმა ა. დიურერმა თავის საუკეთესო გრავიურაში „მელანქოლია“ (1514). დიურერმა გრავიურაზე (ოდნავ შეცვლილ ფორმაში) გაამრავლა იგივე ჯადოსნური კვადრატი, რომელიც შედგება 16 ნომრისგან. 16 3 2 13 5 10 11 8 9 6 7 12 4 15 14 1 ამ ჯადოსნური კვადრატის ხიბლი მხოლოდ ჯამების მუდმივობაში არ არის, რაც მხოლოდ მისი მთავარი საკუთრებაა. ისევე, როგორც ჭეშმარიტად მხატვრულ ნაწარმოებში, რაც უფრო მეტად უყურებ, უფრო ახალ მიმზიდველ ასპექტებს პოულობ, ასევე მათემატიკური ხელოვნების ამ ნაწარმოებში, მთავარის გარდა, ბევრი ლამაზი თვისებაა დამალული.

სლაიდი 8: ა. დიურერის ჯადოსნური კვადრატის თვისებები

თუ ჯადოსნური კვადრატის ყველა სვეტი რიგდება, მათი მონაცვლეობის შენარჩუნებით, ანუ პირველი სვეტის ნომრები განლაგებულია იმავე თანმიმდევრობით, როგორც პირველი მწკრივი, მეორე სვეტის ნომრები, როგორც მეორე რიგი და ა.შ. , მაშინ კვადრატი იგივე თვისებებით ჯადოსნურად დარჩება . რიგებისა და სვეტების გასწვრივ რიცხვების ჯამები, რა თქმა უნდა, არ შეცვლილა, მაგრამ დიაგონალების გასწვრივ რიცხვების ჯამი განსხვავებული გახდა, არ უდრის 34-ს. ჯადოსნურმა კვადრატმა დაკარგა ზოგიერთი ძირითადი თვისება და გახდა "არასრული" ჯადოსნური კვადრატი. (ნახევრად ჯადოსნური მოედანი). როგორც აგრძელებთ კვადრატის რიგებისა და სვეტების შეცვლას, თქვენ მიიღებთ სულ უფრო მეტ ჯადოსნურ და ნახევრად ჯადოსნურ კვადრატებს 16 ნომრისგან. 16 3 2 13 5 10 11 8 9 6 7 12 4 15 14 1 ჯადოსნური კვადრატის ცალკეული სტრიქონების ან სვეტების გაცვლისას, ზოგიერთი ზემოაღნიშნული თვისება შეიძლება გაქრეს, მაგრამ ყველა მათგანი შეიძლება შენარჩუნდეს და ახალიც კი გამოჩნდეს. მაგალითად, თუ გავცვლით ამ კვადრატის პირველ და მეორე სტრიქონებს, მივიღებთ იმას, რაც ნაჩვენებია სურათზე მარჯვნივ: ა. დიურერის ჯადოსნური კვადრატის თვისებები.

სლაიდი 9: რიგის კვადრატები იყოფა ოთხზე

n=4,8,12,4k რიგის ნებისმიერი ჯადოსნური კვადრატის შედგენისთვის, მაგალითად, მოსახერხებელია შემდეგი მარტივი სქემა: მოცემული კვადრატის უჯრებში განათავსეთ რიცხვები ზრდადობით (ბუნებრივი თანმიმდევრობით); შეარჩიეთ ოთხი კვადრატი n/4 გვერდით მოცემული კვადრატის კუთხეებში და ერთი კვადრატი გვერდითი n/2 ცენტრში, არჩეულ ხუთ კვადრატში შეცვალეთ მოცემული კვადრატის ცენტრის მიმართ სიმეტრიულად განლაგებული რიცხვები; ეს ნიშნავს, რომ მეოთხე რიგის კვადრატის რიცხვების ბუნებრივ განლაგებაში უნდა შეიცვალოს 1 და 16, 4 და 13, 6 და 11, 7 და 10. მითითებული სქემის მიხედვით შედგენილი კვადრატები ყოველთვის იქნება მაგიურად სიმეტრიული. 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1